2020-03-23
来源：SME（ID： SMELab）
JohnSlots.com赌场总有着许多“一夜暴富”的神话。在众多造神活动中，数学家封神又最让人信服。
2012 年曾有“澳洲 19 名数学家组团豪赌，狂赢 156 亿”的传闻，但很快就被证明是假消息。
那么数学到底能不能让人在赌场无往不利？
能，只要选对了游戏。
在赌场少有真正的公平，总是庄家赢面略大，但在众多游戏中，还有一种能通过计算概率达到 49% 的胜率。
那就是21点（Blackjack）*，职业赌徒的看家本领。
*注：就像斗地主中的王炸，初始牌拿到A与10则称作“黑杰克（Blackjack）”，直接取胜，这也是21点又名“Blackjack”的原因。
相较于德州扑克、老虎机这些赌场游戏，21 点亲民得多。扑克中两张鬼牌先剔除，其余的牌 2~9 分别记作 2~9 点，10、J、Q、K 记作 10 点，A 视情况记作 1 或 11 点。
游戏的胜负判定很简单，执牌双方将手牌点数相加，通过比大小决定输赢。
总数相加最大只能 21 点，超过 21 点则为“爆牌”直接失败，数字相同则为平局。
而带有赌场特色的 21 点，规则更为繁复。游戏双方分为庄家、玩家，所有玩家只需和庄家比大小。
通常庄家会在半圆形牌桌上应战 5~7 名玩家，因为扑克牌一般也为两副及两副以上。
庄家由赌场方担任，玩家各自决定单局筹码，随后游戏开始！
首回合，玩家与庄家各获得两张初始牌，一张翻开一张合上。
随后而玩家可以选择：拿一张牌（Hit）、结束拿牌（Stand）。
当然，如果局势大好也可以选择赌注翻倍并拿牌（Double）。
还有一种情况，当两张初始牌相同，可将它们分开，另外压一份赌注，再次补充至两张，相当于同一局玩两次（Split）。
如果局势不佳，有的赌场还允许选择认输（Surrender）。
等所有玩家结束拿牌后，庄家看牌，并按规则操作：大等于17点则不拿牌，反之拿牌直至17点，爆牌则所有玩家获胜。
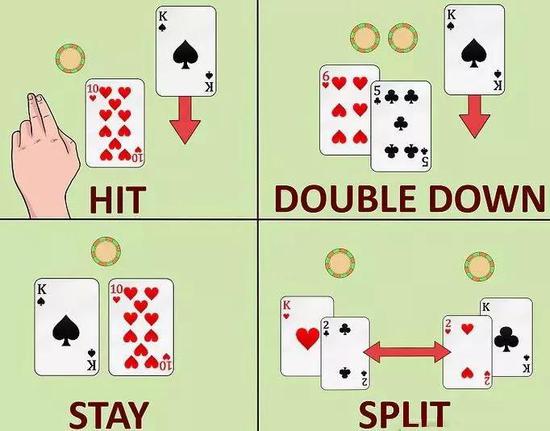21 点并不复杂，感觉更像依靠运气的游戏。但实则不然，21 点的乐趣颇似魔方，不懂的时候只能随意玩玩，一旦把握了公式就像打开了新世界的大门。
作为一款被数学家一直欺负的游戏，绝对是有它好欺负的一面。
1931 年，美国内华达州宣布赌博合法化，21 点开始公开出现在赌博俱乐部，一举成为继骰子游戏后最风行的庄家游戏。
2008 年上映的美国赌博电影《决胜 21 点》，正是围绕 21 点开展的故事。影片中，主角所在的麻省理工学院，有一个秘密团队 Blackjack Team。
这个以高智商成员组建的团队，便是靠着钻研数学技巧在 21 点赌桌上取胜。正是这部电影将赌徒谚语“Winner winner，chicken dinner”，首次捧火。
“21”（2008）电影中的吃鸡大神，在现实中的原型叫马恺文。
马恺文被誉为“华裔赌神”，他凭借团队和数学，在赌场大赚 500 万美元从而名震算牌界。
马恺文在 MIT 读大三时，是个品学兼优的好学生。一次他受邀参加一个 21 点算牌兴趣组，原以为这只是一个以 21 点为攻略对象的数学研讨小组，却不料上了贼船。
马恺文天赋异禀，很快受到神秘教授（从没有人愿意透露他的身份）的认可，成为了小组的核心灵魂。
马恺文（左）随后，被选召的孩子们在教授的带领下，开始到赌场实践。他们不断打磨技术、调整策略，终于走上赢钱道路。第一次赢钱时，马恺文还给自己买了块 2000 美元的手表，一直保留至今。
他们将赌场当提款机，每周就带着 10 万美元去赢几十万美元。赌场也不傻，他们很快被列入黑名单，经常一进场就被服务员“请出”赌场。为了继续提款，他们只得乔装打扮混入场，有时是穿金戴银的土豪、有时是下班发泄欲望的职员……
在 90 年代中期，他们就以 20 来岁的年纪享受在宾馆里数钱为乐的生活。
但 Blackjack Team 所使用的技巧并非什么绝密神技。只需将 21 点的游戏，细细拆分便能理解。
之所以将 21 点说成是赌场最容易赢钱的游戏，是因为在掌握最佳策略的情况下，玩家胜率高达 49% 。而最佳策略也不难掌握，其实就是“算概率”。
假设玩家初始牌点数为12点，庄家明牌为7，计算拿牌与结束拿牌两种选择的胜率。
①选结束拿牌（Stand）时，获胜情况仅一种：
庄家爆牌，设概率为P（S）
庄家的另一张牌有 13 种可能性，概率计算如下
F（T+7）时，庄家不抽牌则不爆牌，不考虑
（以 T 代表10、J、Q、K）
F（9+7）时，抽中 6~T 则爆牌，F（9+7）=8/13
……
以此类推，最终P（S）=∑F=0.26231
②选拿牌（Hit）时，获胜情况两种：
庄家爆牌，玩家不爆；庄家玩家均不爆牌，但玩家更大，设概率为P（H）
爆牌概率同上，但还得算上玩家情况，即（1-4/13）
不爆牌获胜，则有以下可能
1。玩家拿到 21 点，庄家拿到 20~17 点
2。玩家拿到 20 点，庄家拿到 19~17 点
3。玩家拿到 19 点，庄家拿到 18 和 17 点
4。玩家拿到 18 点，庄家拿到 17 点
以最简单的情况 4 作计算
先分析，玩家从 12 到 13，只有抽到 A 一种可能
因此设 W（12）=1
则 W（13）=W（12）*1/13=0.07692
以此可推算 W（18）
而庄家拿 17 点，用同理可算 Z（17）
P4=W（18）+Z（17），同理可算 P1、P2、P3
P（H）=P1+P2+P3+P4+P（S）*9/13=0.43577
对比，P（H）>P（S），因而当玩家手牌为12，庄家明牌为7时，应该选择Hit为最优策略。
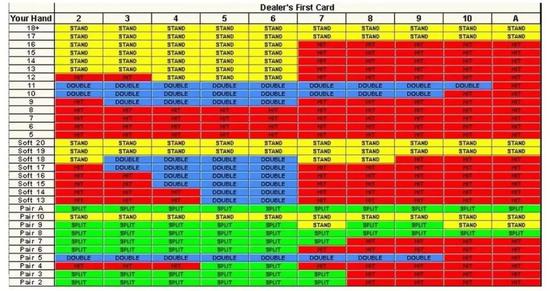所有情况下的选择最优策略能帮玩家做出正确选择，将胜率拉至 49%，数学的威力可见一斑。但明眼人肯定能发现，最优策略也不是很好。
不仅将抽所有牌概率当作 1/13，同时最优策略胜率也不能保证 50% 以上。有什么方法可以再提高一下胜率？这个问题也困扰了不少数学家。
Blackjack 的战术——高低数法是最先突破瓶颈的。
高低法确实诞生于 MIT，但不是马恺文的杰作。
真正的发明人同样传奇，是 MIT 教授爱德华·索普（Edward Thorpe）。就是他开启了数学虐 21 点的时代。
爱德华·索普（Edward Thorpe）索普始终认为，数学是解开赌博的最终密钥。
真正开启 21 点之路的是一篇论文：《二十一点扑克游戏的最佳策略》（Roger Baldwin 著）。
按 Baldwin 的策略估测，以 1 美元一把下注，玩 1000 把也只用交给赌场 6 美元手续费。
索普一学会这套方法，就奔赴拉斯维加斯大展身手，结果吃了好几个月的土。
他决定改进 Baldwin 的方法。
在香农的建议下，他研究出制胜秘诀 1.0，还发表了论文《财富公式：二十一点的制胜秘诀》。
这时纽约最大的庄家找上了他，决定投资他。
他毫不犹豫的答应了，居然真的赢出第一桶金。
随后他写了一本书《战胜赌场》，内容以数学研究为主，将高低数法公诸于世。
所谓高低数法（H-L法）说起来很简单。
将 2~6 记作1，7~9 记作 0，10~A 记作 -1，通过简单的加减法快速记住场上牌的变化。
而高低数法认为，当余下的牌中，大牌越多，则对玩家有利（庄家更容易拿到大牌而爆牌），反之亦然。
例如已经出现了 4、9、10、5、J、A、8，则现在点数是 -1，逆风局。
在实际运用中，还需要计算真数，真数=点数/N 副牌。
如点数为 5，而庄家共使用 5 副牌发牌，则真数为 1。
真数越大赢面越大，真数越小则赢面越小。
因为索普的一本书，当时许多人都去赌场博 21 点。
不过赌场有意防范，真如索普一样封神的并不多。
而且高低数法只不过提高了 2% 的胜率，只有掌握好压注技巧，才能保证一定回合后不亏钱。就算是 Blackjack team，也是经过大量训练，才有可能赚个盆满钵满。
2004年黑杰克世界锦标赛其实，不论是最优策略，还是高低数法，都是为了削弱庄家优势。庄家优势是指在长远期限下，庄家占有数学优势，以确保赌场最终赚钱。
尽管每一次游戏的结果都是随即或是说相互独立的，但总的来说，会趋向一个预期值，或称假设回扣。这也就导致，尽管短期可能赚钱，但长期来说还是会趋向于亏本。
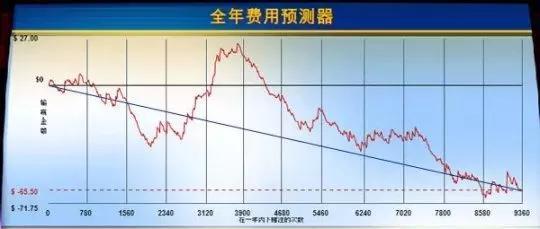黑色直线以上为赚以下为亏，蓝色斜线为假设回扣为了减少这种庄家优势，数学就派上了用场。通过正确的决策思维，规避不必要的错误，夺取百分之几的优势。
但这百分之几投映到长远期限下，回报很惊人。可以说，这就是数学家与赌场数学的一场博弈。
谈及数学的博弈，自然不可避免提到凯利公式。
凯利公式由约翰·凯利于 1956 年在《贝尔系统技术期刊》发表。
凯利公式是为了计算下注比例，当知道获胜率与赔率，可以推算出下注比例以求最大化收益。
John Kelly与他的凯利公式凯利公式的要点就在于如何推算获胜率。
因此凯利提出凯利公式时，就建立在有内线提供获胜率情报的情况下。
但这个公式硬是被他的同事索普运用在 21 点上。
索普不需要内线，用高低数法自己推测情报。
推算获胜率，给出最佳下注比例，大赚一笔。
数学家凭借异乎常人的计算能力自然能与赌场较量一番，同时也说明了一件事：
神仙打架，凡人莫近。
参考资料
Edward Thorp， Beat the Dealer。
Stanford Wong， Blackjack Secrets。
陆振华， 打败赌场。 21世纪经济报道。 2008。
junglerubik， 21点：赌场里最可能赢钱的游戏， 果壳。
