根据量子力学,一个物理系统所处状态用波函数ψ描述。
波函数ψ并不直接对应物理量的取值,我们需要使用算符才能从波函数中把我们关心的物理量的取值“提取”出来。
算符能够把一个函数映射为另一个函数。即:Aψ=φ
我们可定义算符的本征值问题:Aψ=λψ
这里λ是一个数,上式表示算符A把波函数“映射”为自己了,所以这个方程叫本征方程,本征的德语eigen就是“自己”的意思。λ叫本征值,ψ叫λ对应的本征函数。
如果λ是实数,A就是一个厄米算符。
由于物理量都是实数,在量子力学中我们用厄米算符表示物理量。
现在本征方程可以重新写为:
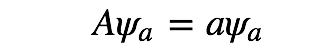
这里a是实数,我们对随便一个波函数ψ做测量A,力图获取物理量A的取值,假如测量是成功的,我们会得到某个a',这个a'就是物理量A的取值。
但如果ψ本身不是A的本征函数,我们需要把ψ对本征函数做个展开,即把ψ表示为好多本征函数的叠加:
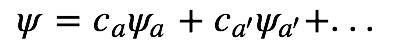
叠加因子是:
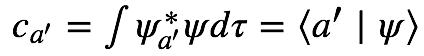
上式中最右侧式子,我已经把结果写成狄拉克记号的形式,可以看出狄拉克记号是非常简洁直观的。
如果ψ不是本征函数的话,我们不能确定每次都能观测到物理量相同的取值。我们只能讲期望,我们期望有多大几率观察到A取a'。
根据玻恩的统计解释,这个几率P是:
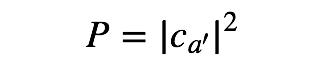
一次成功的测量意味着,波函数ψ坍缩为某个a'对应的本征函数:
![]()
假如我们做连续的测量,因此现在已经是a'对应的本征函数,再做A测量,波函数不变。
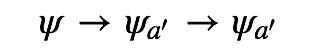
假如我们现在不做A测量,对某个另外的物理量B做测量,假如A,B两个算符对易——[A, B]=0,这意味着存在A、B的共同本征函数:ψab,使得:
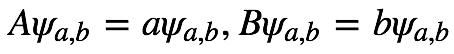
假如我们对共同本征函数ψab做连续的A测量,B测量,我们将得到a,b,并且波函数本身并不因测量而发生改变。
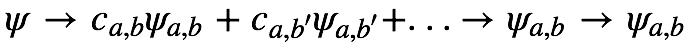
上式中第一个箭头表示做了一个A测量,我们获得的是一系列a确定,但b不确定的本征函数的叠加,然后我们做B测量,我们获得的是a,b都确定下来的本征函数,然后我们再做A测量或B测量,我们读取的物理量A、B的取值将都是a和b。
这就是我们平时所说的如果A、B对易,我们对物理量A、B做测量可以得到同时确定值的意思。
假如A、B不对易,就不存在A、B的共同本征函数,只存在A的本征函数ψa,和B的本征函数φb,假设我们对任意波函数ψ作A测量,如果测量成功,波函数就坍缩为某个A的本征函数ψa,然后我们对ψa作B测量,测量成功,意味着ψa坍缩为某个B的本征函数φb。然后我们再作A测量,由于φb不是A的本征函数,φb要坍缩为某个ψa',这里的a'和a很可能是不一样的,换句话说,我们做的这一系列测量,A的测量值是不确定的。同样的理由,如果我们再接着做B测量的话,b的取值也可能变为不同的b'。
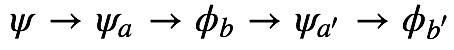
这意味着,假如A、B不对易,就无法同时确定物理量A、B的取值。
比如在量子力学中,位置和动量算符不对易,
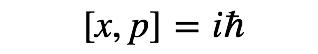
这意味着我们无法同时确定粒子的位置,和粒子的动量。可以证明位置的不确定度Δx和动量的不确定度Δp满足不等式:
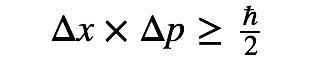
这类不等式不仅仅存在于位置、动量关系,实际上只要算符A、B不对易,我们在数学上可严格证明如下关系:
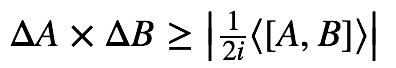
证明过程详见樱井的《现代量子力学》。这意味着当A、B不对易时,对任何波函数我们都无法同时确定A、B的取值。
综上所述,不确定关系与我们的测量技术、测量精度无关,它是量子力学理论体系的自然推论。
现在让我们回到那个著名的比喻,“有一个球,先测得它是白色,后测得它是硬的”,这里的颜色和硬度都是比喻,在大多数教科书中颜色被比喻为测量自旋的z分量Sz,而硬度比喻为测量自旋的x分量Sx,由于Sz和Sx是不对易的,不存在Sz和Sx的共同本征函数。
这意味着当我们知道Sz的取值的时候,我们完全不知道关于Sx的取值,当我们知道Sx的取值的时候,我们完全不知道Sz的取值。
换句话说:对球颜色的测量会完全破坏球硬度的信息,而对球硬度的测量又会完全破坏球颜色的信息。这在字面上当然是违背我们的日常经验的,但这些恰恰是量子世界的基本事实。对事实我们不需要怀疑,需要的是找到恰当的语言去描述它们,量子理论就是可以描述量子世界事实的恰当语言。

 2019-07-28 08:30:31
2019-07-28 08:30:31












