42пјҢдәәзұ»з ҙи§Је®Үе®ҷз”ҹе‘Ҫз»ҲжһҒзӯ”жЎҲпјҢз«ҹжҳҜ3дёӘж•ҙж•°з«Ӣж–№е’Ң
ОДХВАҙФҙЈәжңӘзҹҘ
ЧчХЯЈәиҖҒй“ҒSEO
ИЛЖшЈә10
 2019-09-09 16:54:22
2019-09-09 16:54:22
гҖҖгҖҖжқҘжәҗпјҡж–°жҷәе…ғ
гҖҖгҖҖ[ж–°жҷәе…ғеҜјиҜ»]42пјҢеҸҜд»ҘеҶҷжҲҗ3дёӘж•ҙж•°зҡ„з«Ӣж–№е’ҢпјҒиҝҷжҳҜж•°еӯҰз•Ңзҡ„дёҖеӨ§зӘҒз ҙпјҢз”ұMITе’ҢеёғйҮҢж–ҜжүҳеӨ§еӯҰзҡ„ж•°еӯҰ家е…ұеҗҢеҸ‘зҺ°пјҢ他们д»Ҙ“з”ҹе‘ҪгҖҒе®Үе®ҷд»ҘеҸҠдёҖеҲҮ”зҡ„зҪ‘йЎөж ҮйўҳпјҢе…¬еёғдәҶиҝҷдёҖжҲҗжһңгҖӮ
гҖҖгҖҖдәәзұ»з¬¬дёҖж¬Ўе°Ҷ42еҶҷжҲҗдәҶ3дёӘж•ҙж•°зҡ„з«Ӣж–№е’ҢпјҒ
гҖҖгҖҖжҳЁеӨ©пјҢжңүдәәеңЁ MIT ж•°еӯҰзі»зҡ„зҪ‘з«ҷдёҠиҙҙеҮәдёҖдёӘзӯүејҸпјҢзҪ‘йЎөеҫҲз®ҖеҚ•пјҢдҪҶжІЎз»ҷеҮәз»“жһңпјҡ
гҖҖгҖҖпјҲ-80538738812075974пјү^3 + 80435758145817515^3 + 12602123297335631^3
гҖҖгҖҖзӯүдәҺ 42пјҒ

гҖҖгҖҖеңЁжҺЁзү№дёҠпјҢиҸІе°”е…№еҘ–еҫ—дё»й«ҳе°”ж–Ҝд№ҹиҪ¬еҸ‘дәҶиҝҷдёӘз»“жһңгҖӮ
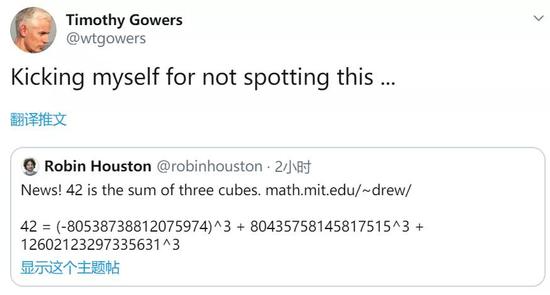
гҖҖгҖҖиҝҷжҳҜдёҖдёӘеӨ§ж–°й—»пјҢеӣ дёәиҮіжӯӨпјҢдёӢйқўиҝҷеҸҘиҜқжҲҗдёәдәҶе®ҡзҗҶпјҡ
гҖҖгҖҖйҷӨдәҶ 9n±4 еһӢиҮӘ然数еӨ–пјҢжүҖжңү 100 д»ҘеҶ…зҡ„иҮӘ然数йғҪиғҪеҶҷжҲҗдёүдёӘж•ҙж•°зҡ„з«Ӣж–№е’ҢгҖӮ
гҖҖгҖҖжҳҜзҡ„пјҢеңЁжӯӨд№ӢеүҚпјҢ42жҳҜ100д»ҘеҶ…жңҖеҗҺдёҖдёӘе°ҡжңӘжүҫеҲ°з«Ӣж–№е’Ңзҡ„ж•ҙж•°и§Јзҡ„иҮӘ然数гҖӮзҺ°еңЁпјҢиҝҷдёӘи§Јд№ҹжүҫеҲ°дәҶгҖӮ
гҖҖгҖҖжүҫеҲ°иҝҷдёӘзӯүејҸзҡ„ж•°еӯҰ家жҳҜжқҘиҮӘеёғйҮҢж–ҜжүҳеӨ§еӯҰзҡ„ Andrew Booker е’ҢжқҘиҮӘйә»зңҒзҗҶе·ҘеӯҰйҷўзҡ„Andrew SutherlandгҖӮ

гҖҖгҖҖAndrew Booker жҳҜеёғйҮҢж–ҜжүҳеӨ§еӯҰж•°еӯҰж•ҷжҺҲ
 Andrew SutherlandжҳҜMITж•°еӯҰзі»йҰ–еёӯз ”з©¶з§‘еӯҰ家
Andrew SutherlandжҳҜMITж•°еӯҰзі»йҰ–еёӯз ”з©¶з§‘еӯҰ家гҖҖгҖҖд»Ҡе№ҙ3жңҲпјҢ Andrew Booker жүҫеҲ°дәҶ33зҡ„з«Ӣж–№е’Ңж•ҙж•°и§ЈпјҢеҗҢж ·еј•иө·ж•°еӯҰз•ҢиҪ°еҠЁгҖӮжҳЁеӨ©пјҢAndrew Bookerз©ҝзқҖеҚ°жңү“42”зҡ„TжҒӨжҺҘеҸ—йҮҮи®ҝпјҢи§ЈйҮҠдәҶ他们зҡ„з ”з©¶иҝҮзЁӢгҖӮ

гҖҖгҖҖеңЁиў«й—®еҲ°“дҪ 们解еҶіиҝҷдёӘй—®йўҳеҗҺпјҢжңүжІЎжңүе…ҙеҘӢеҫ—и·іиө·жқҘ”ж—¶пјҢBookerиҜҙпјҡ“жҲ‘иҝҷж¬ЎеҖ’жҳҜжІЎжңүи·іиө·жқҘпјҢдҪҶжҳҜдҪ зҹҘйҒ“пјҢи§ЈеҶідёҖдёӘдёүгҖҒеӣӣеҚҒе№ҙжқҘдёҖзӣҙжӮ¬иҖҢжңӘеҶізҡ„й—®йўҳпјҢе®һеңЁжҳҜд»ӨдәәеҫҲж»Ўи¶іпјҒеҪ“然пјҢиҝҷдёӘи®әйўҳжң¬иә«иҝҳжІЎжңүи§ЈеҶіпјҢдёӢдёҖдёӘж•°еӯ—жҳҜ114……”
гҖҖгҖҖжңүж„ҸжҖқзҡ„жҳҜпјҢдёӨдҪҚж•°еӯҰ家公еёғиҝҷдёҖз»“жһңзҡ„зҪ‘йЎөж ҮйўҳжҳҜ“з”ҹе‘ҪгҖҒе®Үе®ҷд»ҘеҸҠдёҖеҲҮ”пјҲLifeпјҢ the Universe and EverythingпјүгҖӮ
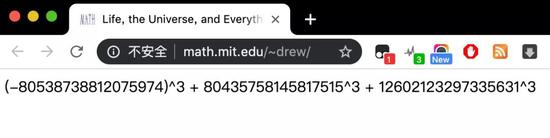 MITзҡ„зҪ‘йЎөжҲӘеӣҫ
MITзҡ„зҪ‘йЎөжҲӘеӣҫгҖҖгҖҖеңЁйҒ“ж јжӢүж–Ҝ·дәҡеҪ“ж–Ҝи‘—еҗҚзҡ„гҖҠ银河系漫游жҢҮеҚ—гҖӢзі»еҲ—дёӯпјҢ42жҳҜ“з”ҹе‘ҪгҖҒе®Үе®ҷд»ҘеҸҠдёҖеҲҮзҡ„з»ҲжһҒзӯ”жЎҲ”гҖӮ
гҖҖгҖҖиҢ«иҢ«е®Үе®ҷдёӯпјҢдёҖдёӘ “е…·жңүи¶…зә§жҷәж…§зҡ„жіӣз»ҙеәҰз§Қж—Ҹ” еҜ№е…ідәҺз”ҹе‘Ҫж„Ҹд№үзҡ„ж— дј‘жӯўзҡ„дәүи®әж„ҹеҲ°еҺҢзғҰдәҶпјҢ他们еҶіе®ҡдёҖеҠіж°ёйҖёең°и§ЈеҶіиҝҷдёӘй—®йўҳгҖӮ他们е»әйҖ дәҶе®Үе®ҷдёҖеҲҮз©әй—ҙе’Ңж—¶й—ҙдёӯ第дәҢејәеӨ§зҡ„з”өи„‘ “жІүжҖқ”пјҢеҗ‘е®ғеҜ»жұӮ “е…ідәҺз”ҹе‘ҪгҖҒе®Үе®ҷпјҢд»ҘеҸҠдёҖеҲҮзҡ„з»ҲжһҒзӯ”жЎҲ”гҖӮ
гҖҖгҖҖж•ҙж•ҙ 750 дёҮе№ҙеҗҺпјҢ“жІүжҖқ” з»ҷеҮәдәҶзӯ”жЎҲ —42гҖӮ
гҖҖгҖҖйқўеҜ№иҝҷдёӘзҺ„еҰҷзҡ„зӯ”жЎҲпјҢжіӣз»ҙеәҰз§Қж—ҸйңҖиҰҒеӣһиҝҮеӨҙе…Ҳеј„жҳҺзҷҪз”ҹе‘Ҫе®Үе®ҷд»ҘеҸҠдёҖеҲҮзҡ„з»ҲжһҒй—®йўҳпјҢж–№иғҪзҗҶи§Јзӯ”жЎҲгҖӮдҪҶ “жІүжҖқ” дёҚиғҪиғңд»»жӯӨйЎ№иү°е·Ёзҡ„д»»еҠЎпјҢе®ғиҜҙпјҡ“дҪ 们йңҖиҰҒдёҖеҸ°иғҪеӨҹи®Ўз®—еҮәиҝҷдёӘз»ҲжһҒзӯ”жЎҲзҡ„з”өи„‘пјҢиҝҷеҸ°з”өи„‘е…·жңүж— йҷҗе’Ңеҫ®еҰҷзҡ„еӨҚжқӮжҖ§пјҢд»ҘиҮідәҺжңүжңәз”ҹе‘Ҫжң¬иә«е°ҶдјҡжҲҗдёәж“ҚдҪңжҜҚдҪ“зҡ„дёҖйғЁеҲҶгҖӮдҪ 们иҮӘиә«д№ҹдјҡд»ҘдёҖз§Қж–°зҡ„з”ҹе‘ҪеҪўејҸжҠ•е…ҘеҲ°иҝҷеҸ°з”өи„‘дёӯпјҢеҺ»ж“ҚжҺ§дёәжңҹ 1000 дёҮе№ҙзҡ„зЁӢеәҸгҖӮжҲ‘е°ҶдјҡдёәдҪ 们и®ҫи®ЎеҮәиҝҷеҸ°з”өи„‘пјҢ并且жҲ‘е·Ідёәе®ғеҸ–еҘҪеҗҚеӯ—гҖӮе®ғе°Ҷдјҡиў«з§°дёә…… ең°зҗғгҖӮ”
гҖҖгҖҖз—ҙиҝ·гҖҒз—ҙзӢӮпјҒдәәзұ»еҜ»жүҫдёүз«Ӣж–№ж•°е’Ңз®ҖеҸІ
гҖҖгҖҖдәәзұ»дёәд»Җд№ҲеҜ№иҝҷж ·дёҖдёӘзӯүејҸеҰӮжӯӨзқҖиҝ·е‘ўпјҹ
гҖҖгҖҖиҝҷдёӘй—®йўҳиҮіе°‘еҸҜд»ҘиҝҪжәҜеҲ° 1825 е№ҙпјҢж•°еӯҰ家жғізҹҘйҒ“пјҢеҰӮжһңз»ҷе®ҡж•ҙж•° KпјҢжҳҜеҗҰеӯҳеңЁж•ҙж•° XгҖҒYгҖҒZпјҢж»Ўи¶іпјҡ
гҖҖгҖҖX^3 + Y^3 + Z^3 = KгҖӮ
гҖҖгҖҖж•°и®әйўҶеҹҹдёӢжңүдёҖеӨ§еҲҶж”ҜеҸ«“дёўз•Әеӣҫж–№зЁӢ”пјҡ

гҖҖгҖҖx^3+y^3+z^3=k жҳҜеҗҰеӯҳеңЁж•ҙж•°и§ЈжҳҜдёўз•Әеӣҫж–№зЁӢдёӯзҡ„дёҖдёӘй—®йўҳгҖӮ
гҖҖгҖҖдёўз•Әеӣҫ пјҲDiophantineпјү жҳҜдёҖдҪҚеҸӨеёҢи…Ҡзҡ„еӨ§ж•°еӯҰ家пјҢиў«и®ӨдёәжҳҜ第дёҖдҪҚжҮӮеҫ—дҪҝз”Ёз¬ҰеҸ·д»ЈиЎЁж•°жқҘз ”з©¶й—®йўҳзҡ„дәәгҖӮ

гҖҖгҖҖдёўз•Әеӣҫе’Ңд»–зҡ„еў“еҝ—й“ӯ
гҖҖгҖҖе…¶дёӯдёўз•ӘеӣҫжңҖи‘—еҗҚзҡ„дәӢиҝ№еҸҜиғҪе°ұжҳҜд»–зҡ„еў“еҝ—й“ӯ —— жӣҫз»Ҹиҝһз»ӯеӨҡе№ҙеҮәзҺ°еңЁеҗ„ең°дёӯе°ҸеӯҰз”ҹзҡ„еҜ’еҒҮдҪңдёҡжү©еұ•и®ӯз»ғдёҠпјҡ
гҖҖгҖҖеқҹдёӯе®ү葬зқҖдёўз•ӘеӣҫгҖӮ
гҖҖгҖҖеӨҡд№Ҳд»ӨдәәжғҠ讶пјҢе®ғеҝ е®һең°и®°еҪ•дәҶжүҖз»ҸеҺҶзҡ„йҒ“и·ҜгҖӮ
гҖҖгҖҖдёҠеёқз»ҷдәҲзҡ„з«Ҙе№ҙеҚ е…ӯеҲҶд№ӢдёҖпјҢ
гҖҖгҖҖеҸҲиҝҮеҚҒдәҢеҲҶд№ӢдёҖпјҢдёӨйўҠй•ҝиғЎпјҢ
гҖҖгҖҖеҶҚиҝҮдёғеҲҶд№ӢдёҖпјҢзӮ№зҮғиө·з»“е©ҡзҡ„иңЎзғӣгҖӮ
гҖҖгҖҖдә”е№ҙд№ӢеҗҺеӨ©иөҗиҙөеӯҗпјҢ
гҖҖгҖҖеҸҜжҖңиҝҹеҲ°зҡ„е®ҒйҰЁе„ҝпјҢдә«е№ҙд»…еҸҠе…¶зҲ¶д№ӢеҚҠпјҢдҫҝиҝӣе…ҘеҶ°еҶ·зҡ„еў“гҖӮ
гҖҖгҖҖжӮІдјӨеҸӘжңүз”Ёж•°и®әзҡ„з ”з©¶еҺ»ејҘиЎҘпјҢ
гҖҖгҖҖеҸҲиҝҮеӣӣе№ҙпјҢд»–д№ҹиө°е®ҢдәҶдәәз”ҹзҡ„ж—…йҖ”гҖӮ
гҖҖгҖҖеӣһеҲ°дёўз•Әеӣҫж–№зЁӢпјҢз”ұдәҺз«Ӣж–№ж•°жЁЎ 9 еҗҢдҪҷ 0гҖҒ1 жҲ– - 1пјҢдёүз«Ӣж–№ж•°е’ҢжЁЎ 9 дёҚеҸҜиғҪеҗҢдҪҷ 4 жҲ– 5пјҢеӣ иҖҢиҝҷжҳҜж•ҙж•°и§ЈеӯҳеңЁзҡ„дёҖдёӘеҝ…иҰҒжқЎд»¶гҖӮеӣ жӯӨ9k+4жҲ–9k+5иҝҷз§ҚеҪўејҸзҡ„ж•ҙж•°дёҚиғҪеҶҷжҲҗдёүдёӘз«Ӣж–№ж•°д№Ӣе’ҢгҖӮ然иҖҢпјҢеҜ№дәҺиҜҘжқЎд»¶жҳҜеҗҰеҗҢж—¶дёәе……еҲҶжқЎд»¶зӣ®еүҚд»ҚжңӘжңүе®ҡи®әгҖӮ
гҖҖгҖҖ1992е№ҙпјҢзүӣжҙҘеӨ§еӯҰзҡ„Roger Heath-BrownжҸҗеҮәзҢңжғіпјҢеҚіе…¶е®ғжүҖжңүж•ҙж•°йғҪеҸҜд»Ҙз”Ёж— з©·еӨҡз§ҚдёҚеҗҢзҡ„ж–№ејҸеҶҷжҲҗдёүдёӘз«Ӣж–№дҪ“зҡ„е’ҢгҖӮеңЁйӮЈд»ҘеҗҺпјҢж•°еӯҰ家们似д№Һе·Із»Ҹиў«Heath-Brownзҡ„и®әзӮ№жүҖиҜҙжңҚпјҢ然иҖҢпјҢжүҫеҲ°жҠҠд»»дҪ•зү№е®ҡзҡ„ж•°еҶҷжҲҗдёүдёӘз«Ӣж–№дҪ“д№Ӣе’Ңзҡ„ж–№жі•д»Қ然жҳҜдёҖдёӘйҡҫйўҳгҖӮ
гҖҖгҖҖ2000е№ҙпјҢе“ҲдҪӣеӨ§еӯҰзҡ„Noam ElkiesжҸҗеҮәдәҶдёҖдёӘе®һз”Ёзҡ„з®—жі•жқҘеҜ»жүҫиҝҷзұ»и§ЈгҖӮElkiesе’Ңе…¶д»–ж•°еӯҰ家дҪҝз”Ёзұ»дјјзҡ„ж–№жі•пјҢжҲҗеҠҹең°дёәи®ёеӨҡиҫғе°Ҹзҡ„ж•ҙж•°жүҫеҲ°дәҶз«Ӣж–№е’Ңзҡ„ж•ҙж•°и§ЈгҖӮ

гҖҖгҖҖ2015е№ҙпјҢж•°еӯҰ家Tim BrowningеҪ•еҲ¶дәҶдёҖж®өи§Ҷйў‘пјҢи§ЈйҮҠдәҶиҝҷдёӘй—®йўҳгҖӮеңЁйӮЈдёӘж—¶еҖҷпјҢеҸӘжңү33гҖҒ42е’Ң74иҝҷдёүдёӘе°ҸдәҺ100зҡ„ж•ҙж•°е°ҡжңӘжүҫеҲ°и§ЈгҖӮиҝҷж®өи§Ҷйў‘и®©жӣҙеӨҡзҡ„дәәжіЁж„ҸеҲ°дәҶиҝҷдёӘй—®йўҳпјҢ并еёҰжқҘдәҶдёҖзі»еҲ—зҡ„зӘҒз ҙгҖӮ
гҖҖгҖҖTim Browningзҡ„и§Ҷйў‘и®©жӣҙеӨҡж•°еӯҰ家关注иҝҷдёӘй—®йўҳ
гҖҖгҖҖеҸ—еҲ°иҝҷж®өи§Ҷйў‘зҡ„еҗҜеҸ‘пјҢеҮ дёӘжңҲеҗҺпјҢSander HuismanжүҫеҲ°дәҶ74зҡ„з«Ӣж–№е’Ңж•ҙж•°и§Јпјҡ

гҖҖгҖҖTim BrowningеҶҚж¬ЎеҪ•еҲ¶дәҶдёҖж®өе…ідәҺHuismanи§ЈеҶі74зҡ„и§Ҷйў‘гҖӮеҸҰдёҖдҪҚж•°еӯҰ家пјҢеҚіеёғйҮҢж–ҜжүҳеӨ§еӯҰзҡ„Andrew BookerзңӢеҲ°дәҶиҝҷж®өи§Ҷйў‘пјҢеҶіе®ҡи§ЈеҶіиҝҷдёӘй—®йўҳгҖӮ
гҖҖгҖҖд»–жҸҗеҮәдәҶдёҖз§Қж–°зҡ„з®—жі•пјҢиҝҷз§Қз®—жі•иғҪжӣҙжңүж•Ҳең°жүҫеҲ°дёҖдёӘзү№е®ҡж•°еӯ—зҡ„и§ЈгҖӮ2019е№ҙ2жңҲ27ж—ҘпјҢBookerе…¬еёғдәҶ33зҡ„з«Ӣж–№е’Ңж•ҙж•°и§ЈгҖӮ
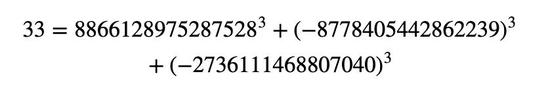
гҖҖгҖҖжҳЁеӨ©пјҢ42д№ҹиў«и§ЈеҶідәҶпјҒAndrew Sutherlandе’ҢAndrew BookerеҗҢж—¶жӣҙ新他们зҡ„дё»йЎөпјҢжҠҘе‘ҠдәҶ42зҡ„з«Ӣж–№е’Ңзҡ„ж•ҙж•°и§Јпјҡ
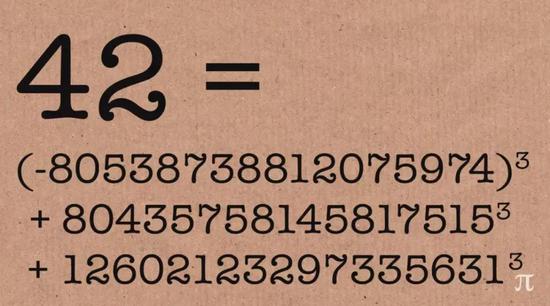
гҖҖгҖҖиҝҷж„Ҹе‘ізқҖ100д»ҘеҶ…зҡ„иҮӘ然数зҡ„з«Ӣж–№е’Ңзҡ„ж•ҙж•°и§Је…ЁйғЁжүҫеҲ°пјҒ
гҖҖгҖҖ1000д»ҘеҶ…иҝҳжІЎжүҫеҲ°и§Јзҡ„ж•ҙж•°еҸӘеү©дёӢпјҡ114пјҢ165пјҢ390пјҢ579пјҢ627пјҢ633пјҢ732пјҢ906пјҢ921 е’Ң 975гҖӮ
гҖҖгҖҖ100 д»ҘеҶ…дёүз«Ӣж–№е’Ңзҡ„йқһйӣ¶и§Је…ЁиЎЁ
гҖҖгҖҖжңҖеҗҺпјҢйҷ„дёҠ 100 д»ҘеҶ…дёүз«Ӣж–№е’Ңзҡ„йқһйӣ¶и§Је…ЁиЎЁпјҲеӨҡз§ҚеҶҷжі•йҖүеҸ–е…¶дёӯдёҖдёӘпјүпјҡ
гҖҖгҖҖ1 = пјҲ-1пјү³ + 1³ + 1³
гҖҖгҖҖ2 = 7³ + пјҲ-5пјү³ + пјҲ-6пјү³
гҖҖгҖҖ3 = 1³ + 1³ + 1³
гҖҖгҖҖ4 дёҚеҸҜиғҪ
гҖҖгҖҖ5 дёҚеҸҜиғҪ
гҖҖгҖҖ6 = пјҲ-1пјү³ + пјҲ-1пјү³ + 2³
гҖҖгҖҖ7 = 104³ + 32³ + пјҲ-105пјү³
гҖҖгҖҖ8 = пјҲ-1пјү³ + 1³ + 2³
гҖҖгҖҖ9 = 217³ + пјҲ-52пјү³ + пјҲ-216пјү³
гҖҖгҖҖ10 = 1³ + 1³ + 2³
гҖҖгҖҖ11 = пјҲ-2пјү³ + пјҲ-2пјү³ + 3³
гҖҖгҖҖ12 = 7³ + 10³ + пјҲ-11пјү³
гҖҖгҖҖ13 дёҚеҸҜиғҪ
гҖҖгҖҖ14 дёҚеҸҜиғҪ
гҖҖгҖҖ15 = пјҲ-1пјү³ + 2³ + 2³
гҖҖгҖҖ16 = пјҲ-511пјү³ + пјҲ-1609пјү³ + 1626³
гҖҖгҖҖ17 = 1³ + 2³ + 2³
гҖҖгҖҖ18 = пјҲ-1пјү³ + пјҲ-2пјү³ + 3³
гҖҖгҖҖ19 = 19³ + пјҲ-14пјү³ + пјҲ-16пјү³
гҖҖгҖҖ20 = 1³ + пјҲ-2пјү³ + 3³
гҖҖгҖҖ21 = пјҲ-11пјү³ + пјҲ-14пјү³ + 16³
гҖҖгҖҖ22 дёҚеҸҜиғҪ
гҖҖгҖҖ23 дёҚеҸҜиғҪ
гҖҖгҖҖ24 = пјҲ-2901096694пјү³ + пјҲ-15550555555пјү³ + 15584139827³
гҖҖгҖҖ25 = пјҲ-1пјү³ + пјҲ-1пјү³ + 3³
гҖҖгҖҖ26 = 297³ + 161³ + пјҲ-312пјү³
гҖҖгҖҖ27 = пјҲ-1пјү³ + 1³ + 3³
гҖҖгҖҖ28 = 14³ + 13³ + пјҲ-17пјү³
гҖҖгҖҖ29 = 1³ + 1³ + 3³
гҖҖгҖҖ30 = пјҲ-283059965пјү³ + пјҲ-2218888517пјү³ + 2220422932³
гҖҖгҖҖ31 дёҚеҸҜиғҪ
гҖҖгҖҖ32 дёҚеҸҜиғҪ
гҖҖгҖҖ33 = 8866128975287528³ + пјҲ-8778405442862239пјү³ + пјҲ-2736111468807040пјү³
гҖҖгҖҖ34 = пјҲ-1пјү³ + 2³ + 3³
гҖҖгҖҖ35 = 14³ + пјҲ-8пјү³ + пјҲ-13пјү³
гҖҖгҖҖ36 = 1³ + 2³ + 3³
гҖҖгҖҖ37 = 50³ + 37³ + пјҲ-56пјү³
гҖҖгҖҖ38 = 1³ + пјҲ-3пјү³ + 4³
гҖҖгҖҖ39 = 117367³ + 134476³ + пјҲ-159380пјү³
гҖҖгҖҖ40 дёҚеҸҜиғҪ
гҖҖгҖҖ41 дёҚеҸҜиғҪ
гҖҖгҖҖ42 = пјҲ-80538738812075974пјү³ + 80435758145817515³ + 12602123297335631³
гҖҖгҖҖ43 = 2³ + 2³ + 3³
гҖҖгҖҖ44 = пјҲ-5пјү³ + пјҲ-7пјү³ + 8³
гҖҖгҖҖ45 = 2³ + пјҲ-3пјү³ + 4³
гҖҖгҖҖ46 = пјҲ-2пјү³ + 3³ + 3³
гҖҖгҖҖ47 = 6³ + 7³ + пјҲ-8пјү³
гҖҖгҖҖ48 = пјҲ-23пјү³ + пјҲ-26пјү³ + 31³
гҖҖгҖҖ49 дёҚеҸҜиғҪ
гҖҖгҖҖ50 дёҚеҸҜиғҪ
гҖҖгҖҖ51 = 602³ + 659³ + пјҲ-796пјү³
гҖҖгҖҖ52 = 23961292454³ + 60702901317³ + пјҲ-61922712865пјү³
гҖҖгҖҖ53 = пјҲ-1пјү³ + 3³ + 3³
гҖҖгҖҖ54 = пјҲ-7пјү³ + пјҲ-11пјү³ + 12³
гҖҖгҖҖ55 = 1³ + 3³ + 3³
гҖҖгҖҖ56 = пјҲ-11пјү³ + пјҲ-21пјү³ + 22³
гҖҖгҖҖ57 = 1³ + пјҲ-2пјү³ + 4³
гҖҖгҖҖ58 дёҚеҸҜиғҪ
гҖҖгҖҖ59 дёҚеҸҜиғҪ
гҖҖгҖҖ60 = пјҲ-1пјү³ + пјҲ-4пјү³ + 5³
гҖҖгҖҖ61 = 845³ + 668³ + пјҲ-966пјү³
гҖҖгҖҖ62 = 3³ + 3³ + 2³
гҖҖгҖҖ63 = 7³ + пјҲ-4пјү³ + пјҲ-6пјү³
гҖҖгҖҖ64 = пјҲ-1пјү³ + 1³ + 4³
гҖҖгҖҖ65 = 91³ + 85³ + пјҲ-111пјү³
гҖҖгҖҖ66 = 1³ + 1³ + 4³
гҖҖгҖҖ67 дёҚеҸҜиғҪ
гҖҖгҖҖ68 дёҚеҸҜиғҪ
гҖҖгҖҖ69 = 2³ + пјҲ-4пјү³ + 5³
гҖҖгҖҖ70 = 11³ + 20³ + пјҲ-21пјү³
гҖҖгҖҖ71 = пјҲ-1пјү³ + 2³ + 4³
гҖҖгҖҖ72 = 7³ + 9³ + пјҲ-10пјү³
гҖҖгҖҖ73 = 1³ + 2³ + 4³
гҖҖгҖҖ74 = пјҲ-284650292555885пјү³ + пјҲ66229832190556пјү³ + пјҲ283450105697727пјү³
гҖҖгҖҖ75 = 4381159³ + 435203083³ + пјҲ-435203231пјү³
гҖҖгҖҖ76 дёҚеҸҜиғҪ
гҖҖгҖҖ77 дёҚеҸҜиғҪ
гҖҖгҖҖ78 = 26³ + 53³ + пјҲ-55пјү³
гҖҖгҖҖ79 = пјҲ-19пјү³ + пјҲ-33пјү³ + 35³
гҖҖгҖҖ80 = 69241³ + 103532³ + пјҲ-112969пјү³
гҖҖгҖҖ81 = 10³ + 17³ + пјҲ-18пјү³
гҖҖгҖҖ82 = пјҲ-11пјү³ + пјҲ-11пјү³ + 14³
гҖҖгҖҖ83 = пјҲ-2пјү³ + 3³ + 4³
гҖҖгҖҖ84 = пјҲ-8241191пјү³ + пјҲ-41531726пјү³ + 41639611³
гҖҖгҖҖ85 дёҚеҸҜиғҪ
гҖҖгҖҖ86 дёҚеҸҜиғҪ
гҖҖгҖҖ87 = пјҲ-1972пјү³ + пјҲ-4126пјү³ + 4271³
гҖҖгҖҖ88 = 3³ + пјҲ-4пјү³ + 5³
гҖҖгҖҖ89 = 6³ + 6³ + пјҲ-7пјү³
гҖҖгҖҖ90 = пјҲ-1пјү³ + 3³ + 4³
гҖҖгҖҖ91 = 364³ + 192³ + пјҲ-381пјү³
гҖҖгҖҖ92 = 1³ + 3³ + 4³
гҖҖгҖҖ93 = пјҲ-5пјү³ + пјҲ-5пјү³ + 7³
гҖҖгҖҖ94 дёҚеҸҜиғҪ
гҖҖгҖҖ95 дёҚеҸҜиғҪ
гҖҖгҖҖ96 = 10853³ + 13139³ + пјҲ-15250пјү³
гҖҖгҖҖ97 = пјҲ-1пјү³ + пјҲ-3пјү³ + 5³
гҖҖгҖҖ98 = 14³ + 9³ + пјҲ-15пјү³
гҖҖгҖҖ99 = 2³ + 3³ + 4³
гҖҖгҖҖ100 = 7³ + пјҲ-3пјү³ + пјҲ-6пјү³
дёҠдёҖзҜҮпјҡзҷҪиЎҖз—…жІ»ж„ҲзҺҮ80%пјҹж—Ҙжң¬зҡ„иҝҷж¬ҫж–°иҚҜжІЎйӮЈд№ҲзҘһ
дёӢдёҖзҜҮпјҡзҺӢиҙ»иҠіиҺ·пјӮжңӘжқҘ科еӯҰеӨ§еҘ–пјӮпјҢ笑称е»әеҜ№ж’һжңәиҝңиҝңдёҚеӨҹ













