tensorflow集成和实现了各种机器学习基础的算法,可以直接调用。
代码集:https://github.com/ageron/handson-ml
监督学习
1)决策树(Decision Tree)和随机森林
决策树:
决策树是一种树形结构,为人们提供决策依据,决策树可以用来回答yes和no问题,它通过树形结构将各种情况组合都表示出来,每个分支表示一次选择(选择yes还是no),直到所有选择都进行完毕,最终给出正确答案。
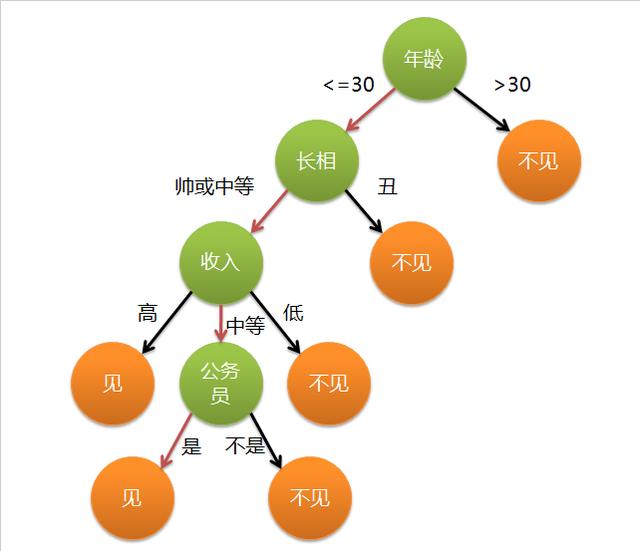
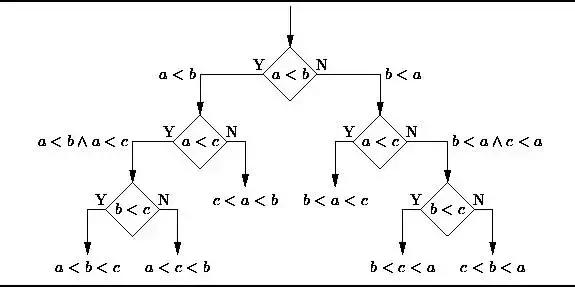
决策树(decision tree)是一个树结构(可以是二叉树或非二叉树)。在实际构造决策树时,通常要进行剪枝,这时为了处理由于数据中的噪声和离群点导致的过分拟合问题。剪枝有两种:
先剪枝——在构造过程中,当某个节点满足剪枝条件,则直接停止此分支的构造。
后剪枝——先构造完成完整的决策树,再通过某些条件遍历树进行剪枝。
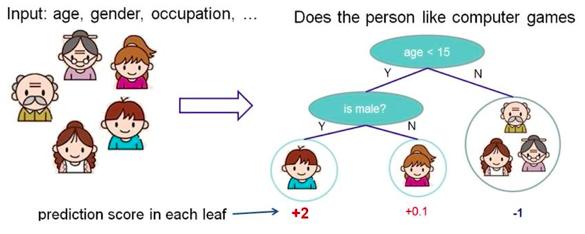
决策树主要是调用sklearn里面函数,这个里面包含了DecisionTreeClassifier,不需要我们自己去实现。
import numpy as np import matplotlib.pyplot as plt from sklearn.tree import DecisionTreeRegressor if __name__ == "__main__": n = 500 x = np.random.rand(n) * 8 - 3 x.sort() y = np.cos(x) + np.sin(x) + np.random.randn(n) * 0.4 x = x.reshape(-1, 1) reg = DecisionTreeRegressor(criterion='mse') # reg1 = RandomForestRegressor(criterion='mse') dt = reg.fit(x, y) # dt1 = reg1.fit(x, y) x_test = np.linspace(-3, 5, 100).reshape(-1, 1) y_hat = dt.predict(x_test) plt.figure(facecolor="w") plt.plot(x, y, 'ro', label="actual") plt.plot(x_test, y_hat, 'k*', label="predict") plt.legend(loc="best") plt.title(u'Decision Tree', fontsize=17) plt.tight_layout() plt.grid() plt.show()
随机森林:
1. Bagging
Bootstrap:一种有放回的抽样方法。
Bagging( bootstrap aggregation)的策略:从样本集中进行有放回地选出n个样本;在样本的所有特征上,对这n个样本建立分类器;重复上述两步m次,获得m个样本分类器;最后将测试数据都放在这m个样本分类器上,最终得到m个分类结果,再从这m个分类结果中决定数据属于哪一类(多数投票制)。
随机森林采用了Bagging策略,且在其基础上进行了一些修改,采用了两个随机:
- 从训练样本集中使用Bootstrap采样(随机有放回)选出n个样本。
- 设样本共有b个特征,从这b个特征中只随机选择k个特征来分割样本,通过计算选择最优划分特征作为节点来划分样本集合来建立决策树。(与Bagging的不同之处:没有使用全部的特征,这样可以避免一些过拟合的特征,不再对决策树进行任何剪枝)
- 重复以上两步m次,可建立m棵决策树
- 这m棵决策树形成了森林,可通过简单多数投票法(或其他投票机制)来决定森林的输出,决定属于哪一类型。(针对解决回归问题,可以采用单棵树输出结果总和的平均值)
随机森林在一定程序上提高了泛化能力,而且可以并行地生成单棵树。
代码示例:使用决策树和随机森林进行手写数字(sklearn中的digits数据)的预测:
from sklearn import datasets
from sklearn.model_selection import cross_val_score
import datetime
from sklearn import tree
from sklearn.ensemble import RandomForestClassifier
digits = datasets.load_digits();
X = digits.data\
# // 特征矩阵
y = digits.target \
# // 标签矩阵
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=1/3., random_state=8) \
# // 分割训练集和测试集
estimators = {}
# criterion: 分支的标准(gini/entropy)
estimators['tree'] = tree.DecisionTreeClassifier(criterion='gini',random_state=8) # 决策树
# n_estimators: 树的数量
# bootstrap: 是否随机有放回
# n_jobs: 可并行运行的数量
estimators['forest'] = RandomForestClassifier(n_estimators=20,criterion='gini',bootstrap=True,n_jobs=2,random_state=8) # 随机森林
for k in estimators.keys():
start_time = datetime.datetime.now()
# print '----%s----' % k
estimators[k] = estimators[k].fit(X_train, y_train)
pred = estimators[k].predict(X_test)
# print pred[:10]
print("%s Score: %0.2f" % (k, estimators[k].score(X_test, y_test)))
scores = cross_val_score(estimators[k], X_train, y_train,scoring='accuracy' ,cv=10)
print("%s Cross Avg. Score: %0.2f (+/- %0.2f)" % (k, scores.mean(), scores.std() * 2))
end_time = datetime.datetime.now()
time_spend = end_time - start_time
print("%s Time: %0.2f" % (k, time_spend.total_seconds()))
2)朴素贝叶斯分类器(Naive Bayesian Model,NBM)
朴素贝叶斯分类器基于贝叶斯定理及其假设(即特征之间是独立的,是不相互影响的),主要用来解决分类和回归问题。
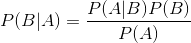
P(A|B) 是后验概率, P(B|A) 是似然,P(A)为先验概率,P(B) 为我们要预测的值。
具体应用有:标记一个电子邮件为垃圾邮件或非垃圾邮件;将新闻文章分为技术类、政治类或体育类;检查一段文字表达积极的情绪,或消极的情绪;用于人脸识别软件。
学过概率的同学一定都知道贝叶斯定理,这个在250多年前发明的算法,在信息领域内有着无与伦比的地位。贝叶斯分类是一系列分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。朴素贝叶斯算法(Naive Bayesian) 是其中应用最为广泛的分类算法之一。朴素贝叶斯分类器基于一个简单的假定:给定目标值时属性之间相互条件独立。
通过以上定理和“朴素”的假定,我们知道:
P( Category | Document) = P ( Document | Category ) * P( Category) / P(Document)
举个例子,给一段文字,返回情感分类,这段文字的态度是positive,还是negative。

为了解决这个问题,可以只看其中的一些单词。

这段文字,将仅由一些单词和它们的计数代表。
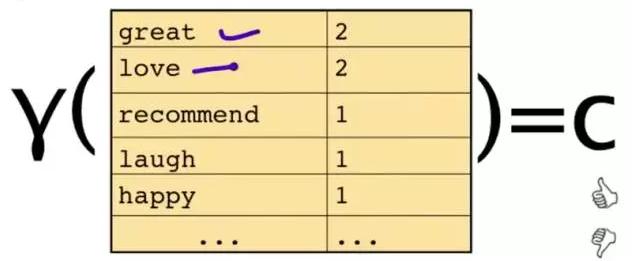
原始问题是:给你一句话,它属于哪一类?
通过 bayes rules 变成一个比较简单容易求得的问题。

问题变成,这一类中这句话出现的概率是多少,当然,别忘了公式里的另外两个概率。
例子:单词love在positive 的情况下出现的概率是0.1,在negative的情况下出现的概率是 0.001。
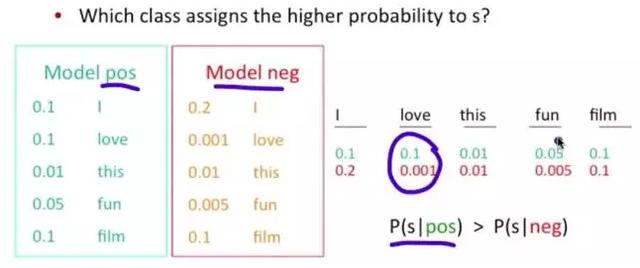
后面将给大家详细讲解朴素贝叶斯分类算法。
实际应用场景
- 文本分类
- 垃圾邮件过滤
- 病人分类
- 拼写检查
朴素贝叶斯模型
朴素贝叶斯常用的三个模型有:
- 高斯模型:处理特征是连续型变量的情况
- 多项式模型:最常见,要求特征是离散数据
- 伯努利模型:要求特征是离散的,且为布尔类型,即true和false,或者1和0
基于多项式模型的朴素贝叶斯算法(在github获取)
# encoding=utf-8
import pandas as pd
import numpy as np
import cv2
import time
from sklearn.cross_validation import train_test_split
from sklearn.metrics import accuracy_score
# 二值化处理
def binaryzation(img):
cv_img = img.astype(np.uint8) # 类型转化成Numpy中的uint8型
cv2.threshold(cv_img, 50, 1, cv2.THRESH_BINARY_INV, cv_img) # 大于50的值赋值为0,不然赋值为1
return cv_img
# 训练,计算出先验概率和条件概率
def Train(trainset, train_labels):
prior_probability = np.zeros(class_num) # 先验概率
conditional_probability = np.zeros((class_num, feature_len, 2)) # 条件概率
# 计算
for i in range(len(train_labels)):
img = binaryzation(trainset[i]) # 图片二值化,让每一个特征都只有0,1两种取值
label = train_labels[i]
prior_probability[label] += 1
for j in range(feature_len):
conditional_probability[label][j][img[j]] += 1
# 将条件概率归到[1,10001]
for i in range(class_num):
for j in range(feature_len):
# 经过二值化后图像只有0,1两种取值
pix_0 = conditional_probability[i][j][0]
pix_1 = conditional_probability[i][j][1]
# 计算0,1像素点对应的条件概率
probalility_0 = (float(pix_0)/float(pix_0+pix_1))*10000 + 1
probalility_1 = (float(pix_1)/float(pix_0+pix_1))*10000 + 1
conditional_probability[i][j][0] = probalility_0
conditional_probability[i][j][1] = probalility_1
return prior_probability, conditional_probability
# 计算概率
def calculate_probability(img, label):
probability = int(prior_probability[label])
for j in range(feature_len):
probability *= int(conditional_probability[label][j][img[j]])
return probability
# 预测
def Predict(testset, prior_probability, conditional_probability):
predict = []
# 对每个输入的x,将后验概率最大的类作为x的类输出
for img in testset:
img = binaryzation(img) # 图像二值化
max_label = 0
max_probability = calculate_probability(img, 0)
for j in range(1, class_num):
probability = calculate_probability(img, j)
if max_probability < probability:
max_label = j
max_probability = probability
predict.append(max_label)
return np.array(predict)
class_num = 10 # MINST数据集有10种labels,分别是“0,1,2,3,4,5,6,7,8,9”
feature_len = 784 # MINST数据集每个image有28*28=784个特征(pixels)
if __name__ == '__main__':
print("Start read data")
time_1 = time.time()
raw_data = pd.read_csv('../data/train.csv', header=0) # 读取csv数据
data = raw_data.values
features = data[::, 1::]
labels = data[::, 0]
# 避免过拟合,采用交叉验证,随机选取33%数据作为测试集,剩余为训练集
train_features, test_features, train_labels, test_labels = train_test_split(features, labels, test_size=0.33, random_state=0)
time_2 = time.time()
print('read data cost %f seconds' % (time_2 - time_1))
print('Start training')
prior_probability, conditional_probability = Train(train_features, train_labels)
time_3 = time.time()
print('training cost %f seconds' % (time_3 - time_2))
print('Start predicting')
test_predict = Predict(test_features, prior_probability, conditional_probability)
time_4 = time.time()
print('predicting cost %f seconds' % (time_4 - time_3))
score = accuracy_score(test_labels, test_predict)
print("The accruacy score is %f" % score)
3)最小二乘法(Least squares)
如果你对统计学有所了解,那么你必定听说过线性回归。最小均方就是用来求线性回归的。如下图所示,平面内会有一系列点,然后我们求取一条线,使得这条线尽可能拟合这些点分布,这就是线性回归。这条线有多种找法,最小二乘法就是其中一种。最小二乘法其原理如下,找到一条线使得平面内的所有点到这条线的欧式距离和最小。这条线就是我们要求取得线。
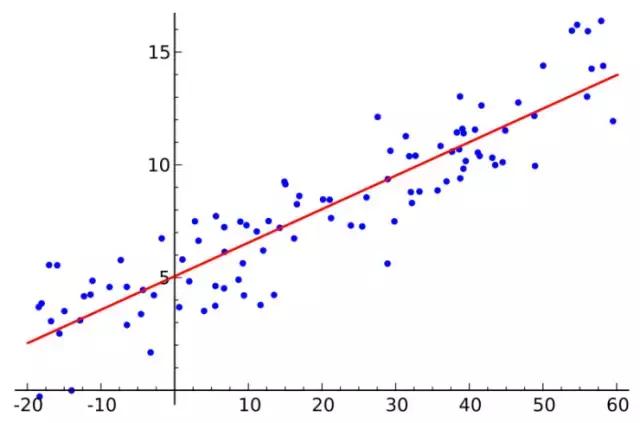
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
4)逻辑回归(Logistic Regression)
逻辑回归模型是一个二分类模型,它选取不同的特征与权重来对样本进行概率分类,用一个log函数计算样本属于某一类的概率。即一个样本会有一定的概率属于一个类,会有一定的概率属于另一类,概率大的类即为样本所属类。用于估计某种事物的可能性。
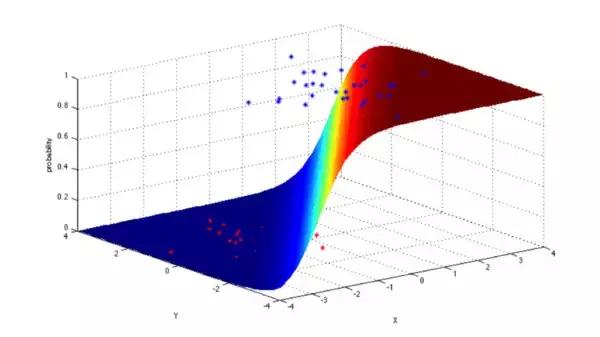
5)支持向量机(SVM)
支持向量机(support vector machine)是一个二分类算法,它可以在N维空间找到一个(N-1)维的超平面,这个超平面可以将这些点分为两类。也就是说,平面内如果存在线性可分的两类点,SVM可以找到一条最优的直线将这些点分开。SVM应用范围很广。
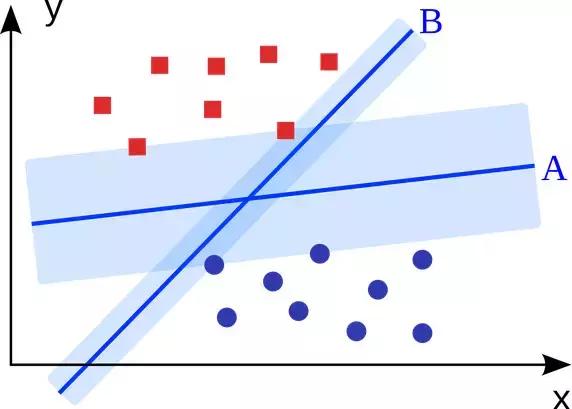
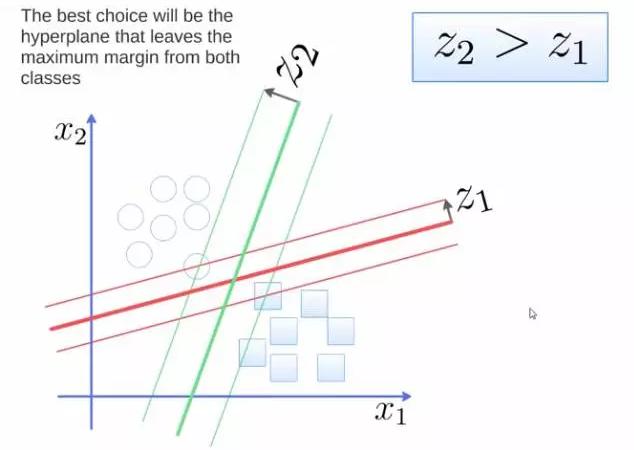
要将两类分开,想要得到一个超平面,最优的超平面是到两类的margin达到最大,margin就是超平面与离它最近一点的距离,如下图,Z2>Z1,所以绿色的超平面比较好。
6)K最近邻算法(KNN,K-NearestNeighbor)
邻近算法,或者说K最近邻(KNN,K-NearestNeighbor)分类算法是数据挖掘分类技术中最简单的方法之一。KNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 KNN方法在类别决策时,只与极少量的相邻样本有关。由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
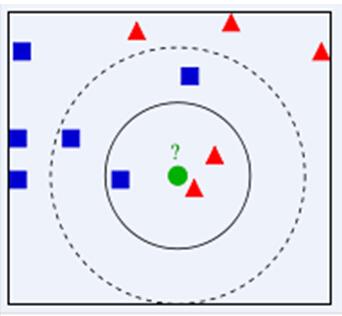
主要应用领域是对未知事物的识别,即判断未知事物属于哪一类,判断思想是,基于欧几里得定理,判断未知事物的特征和哪一类已知事物的的特征最接近。如上图,绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形?如果K=3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,如果K=5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。由此也说明了KNN算法的结果很大程度取决于K的选择。
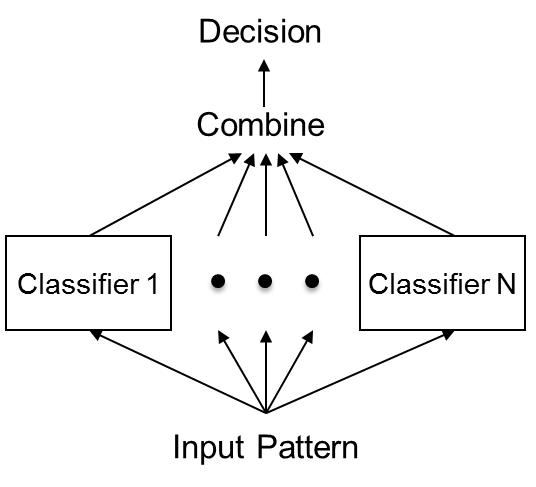
7)集成学习(Ensemble Learning)
集成学习就是将很多分类器集成在一起,每个分类器有不同的权重,将这些分类器的分类结果合并在一起,作为最终的分类结果。最初集成方法为贝叶斯决策。
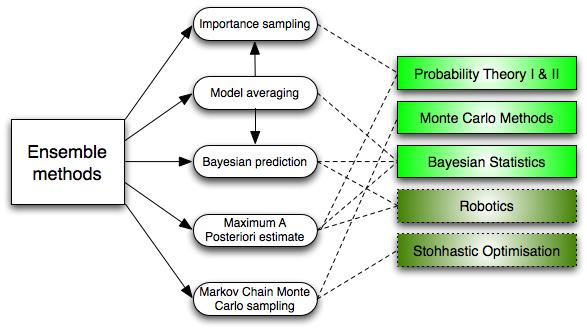
集成算法用一些相对较弱的学习模型独立地就同样的样本进行训练,然后把结果整合起来进行整体预测。集成算法的主要难点在于究竟集成哪些独立的较弱的学习模型以及如何把学习结果整合起来。这是一类非常强大的算法,同时也非常流行。常见的算法包括:Boosting, Bootstrapped Aggregation(Bagging), AdaBoost,堆叠泛化(Stacked Generalization, Blending),梯度推进机(Gradient Boosting Machine, GBM),随机森林(Random Forest)。
那么集成方法是怎样工作的,为什么他们会优于单个的模型?
- 他们拉平了输出偏差:如果你将具有民主党倾向的民意调查和具有共和党倾向的民意调查取平均,你将得到一个中和的没有倾向一方的结果。
- 它们减小了方差:一堆模型的聚合结果和单一模型的结果相比具有更少的噪声。在金融领域,这被称为多元化——多只股票的混合投资要比一只股票变化更小。这就是为什么数据点越多你的模型会越好,而不是数据点越少越好。
- 它们不太可能产生过拟合:如果你有一个单独的没有过拟合的模型,你是用一种简单的方式(平均,加权平均,逻辑回归)将这些预测结果结合起来,然后就没有产生过拟合的空间了。
无监督学习
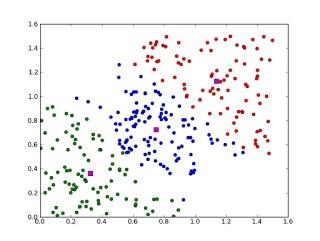
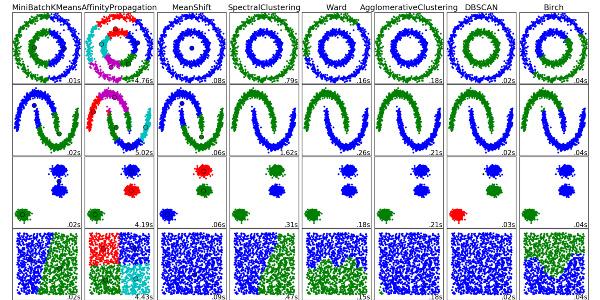
8)聚类算法
聚类算法就是将一堆数据进行处理,根据它们的相似性对数据进行聚类。
聚类,就像回归一样,有时候人们描述的是一类问题,有时候描述的是一类算法。聚类算法通常按照中心点或者分层的方式对输入数据进行归并。所以的聚类算法都试图找到数据的内在结构,以便按照最大的共同点将数据进行归类。常见的聚类算法包括 k-Means算法以及期望最大化算法(Expectation Maximization, EM)。
聚类算法有很多种,具体如下:中心聚类、关联聚类、密度聚类、概率聚类、降维、神经网络/深度学习。
9)K-均值算法(K-Means)
K-means算法是硬聚类算法,是典型的基于原型的目标函数聚类方法的代表,它是数据点到原型的某种距离作为优化的目标函数,利用函数求极值的方法得到迭代运算的调整规则。K-means算法以欧式距离作为相似度测度,它是求对应某一初始聚类中心向量V最优分类,使得评价指标J最小。算法采用误差平方和准则函数作为聚类准则函数。K-means算法是很典型的基于距离的聚类算法,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。
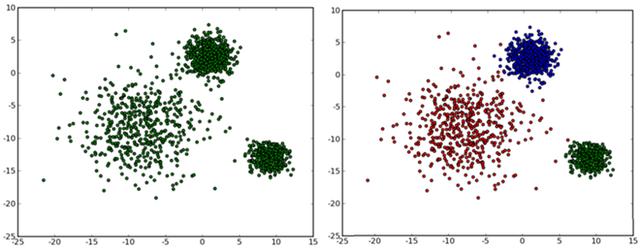
通常,人们根据样本间的某种距离或者相似性来定义聚类,即把相似的(或距离近的)样本聚为同一类,而把不相似的(或距离远的)样本归在其他类。
10)主成分分析(Principal Component Analysis,PCA)
主成分分析是利用正交变换将一些列可能相关数据转换为线性无关数据,从而找到主成分。PCA方法最著名的应用应该是在人脸识别中特征提取及数据降维。
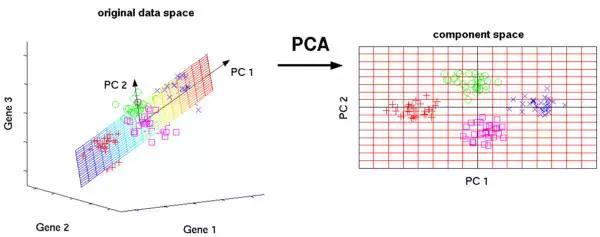
PCA主要用于简单学习与可视化中数据压缩、简化。但是PCA有一定的局限性,它需要你拥有特定领域的相关知识。对噪音比较多的数据并不适用。
11)SVD矩阵分解(Singular Value Decomposition)
也叫奇异值分解(Singular Value Decomposition),是线性代数中一种重要的矩阵分解,是矩阵分析中正规矩阵酉对角化的推广。在信号处理、统计学等领域有重要应用。SVD矩阵是一个复杂的实复负数矩阵,给定一个m行、n列的矩阵M,那么M矩阵可以分解为M = UΣV。U和V是酉矩阵,Σ为对角阵。
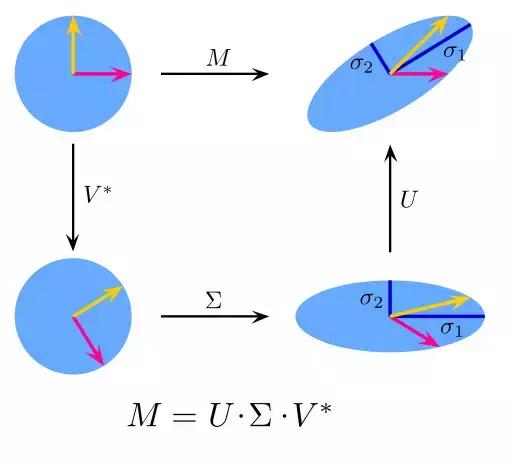
PCA实际上就是一个简化版本的SVD分解。在计算机视觉领域,第一个脸部识别算法就是基于PCA与SVD的,用特征对脸部进行特征表示,然后降维、最后进行面部匹配。尽管现在面部识别方法复杂,但是基本原理还是类似的。
12)独立成分分析(ICA)
独立成分分析(Independent Component Analysis,ICA)是一门统计技术,用于发现存在于随机变量下的隐性因素。ICA为给观测数据定义了一个生成模型。在这个模型中,其认为数据变量是由隐性变量,经一个混合系统线性混合而成,这个混合系统未知。并且假设潜在因素属于非高斯分布、并且相互独立,称之为可观测数据的独立成分。
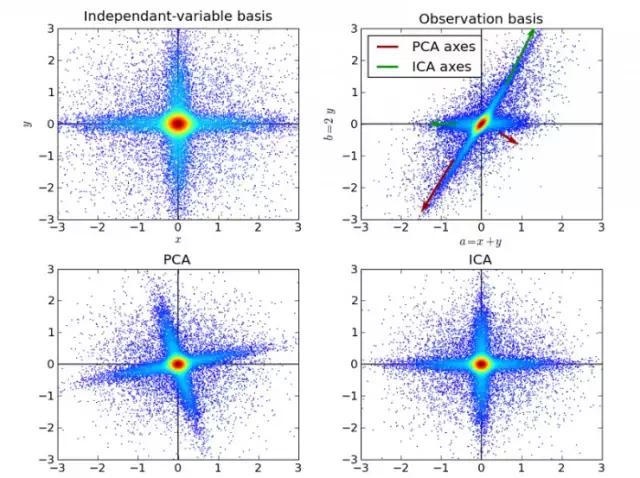
ICA与PCA相关,但它在发现潜在因素方面效果良好。它可以应用在数字图像、档文数据库、经济指标、心里测量等。

上图为基于ICA的人脸识别模型。实际上这些机器学习算法并不是全都像想象中一样复杂,有些还和高中数学紧密相关。
后面讲给大家一一详细单独讲解这些常用算法。
强化学习
13)Q-Learning算法
Q-learning要解决的是这样的问题:一个能感知环境的自治agent,怎样通过学习选择能达到其目标的最优动作。
强化学习目的是构造一个控制策略,使得Agent行为性能达到最大。Agent从复杂的环境中感知信息,对信息进行处理。Agent通过学习改进自身的性能并选择行为,从而产生群体行为的选择,个体行为选择和群体行为选择使得Agent作出决策选择某一动作,进而影响环境。增强学习是指从动物学习、随机逼近和优化控制等理论发展而来,是一种无导师在线学习技术,从环境状态到动作映射学习,使得Agent根据最大奖励值采取最优的策略;Agent感知环境中的状态信息,搜索策略(哪种策略可以产生最有效的学习)选择最优的动作,从而引起状态的改变并得到一个延迟回报值,更新评估函数,完成一次学习过程后,进入下一轮的学习训练,重复循环迭代,直到满足整个学习的条件,终止学习。
Q-Learning是一种无模型的强化学习技术。具体来说,可以使用Q学习来为任何给定的(有限的)马尔可夫决策过程(MDP)找到最优的动作选择策略。它通过学习一个动作价值函数,最终给出在给定状态下采取给定动作的预期效用,然后遵循最优策略。一个策略是代理在选择动作后遵循的规则。当这种动作值函数被学习时,可以通过简单地选择每个状态中具有最高值的动作来构建最优策略。 Q-learning的优点之一是能够比较可用操作的预期效用,而不需要环境模型。此外,Q学习可以处理随机过渡和奖励的问题,而不需要任何适应。已经证明,对于任何有限的MDP,Q学习最终找到一个最优策略,从总体奖励的预期值返回到从当前状态开始的所有连续步骤是最大可实现的意义。

 2019-08-12 08:51:41
2019-08-12 08:51:41












