2021-03-26 04:39:21
欧拉公式（英语：Euler’s formula，又称尤拉公式）是在复分析领域的公式，将三角函数与复数指数函数相关联，因其提出者莱昂哈德·欧拉而得名。尤拉公式提出，对任意实数 xx，都存在:
ejx=cosx+jsinx
其中jj是虚数单位。
由上式，我们可以推导出：
sin?=12j(ej??e?j?)
cos??=12(ej?+e?j?)
证明：
有许多方式可以证明欧拉公式，这里仅用泰勒级数进行证明，其他方式可以参考Wiki欧拉公式
在知乎上看到了Heinrich写的一篇关于傅里叶变换的文章，让我茅塞顿开，惊叹数学的美丽和神奇，文章中介绍了复数的意义，我觉得讲的很好，故记录下来：
虚数i这个概念大家在高中就接触过，但那时我们只知道它是-1的平方根，可是它真正的意义是什么呢?
这里有一条数轴，在数轴上有一个红色的线段，它的长度是1。当它乘以3的时候，它的长度发生了变化，变成了蓝色的线段，而当它乘以-1的时候，就变成了绿色的线段，或者说线段在数轴上围绕原点旋转了180度。
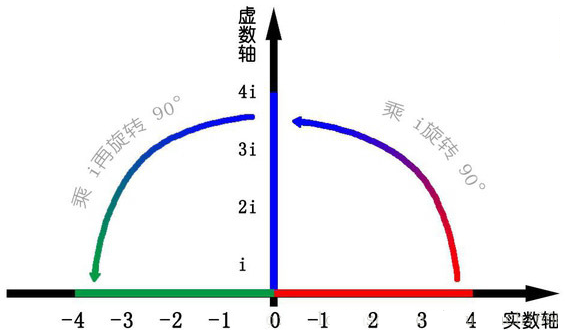
我们知道乘-1其实就是乘了两次 i使线段旋转了180度，那么乘一次 i 呢——答案很简单——旋转了90度。
