概述
手写排序算法几乎是程序员面试必问的题目,大多数人都会选择写冒泡排序,如果此时你写的是其他改进过的排序算法,相信会让面试官眼前一亮。本文将介绍常见的排序算法中的“快速排序”。
基本思想
快速排序(QuickSort)是对冒泡排序的一种改进。快速排序由C. A. R. Hoare在1962年提出。它的基本思想是:
从要排序的数据中取一个数为“基准数”。
通过一趟排序将要排序的数据分割成独立的两部分,其中左边的数据都比“基准数”小,右边的数据都比“基准数”大。
然后再按步骤2对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
该思想可以概括为:挖坑填数 + 分治法。
分治法
分治,字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。在计算机科学中,分治法就是运用分治思想的一种很重要的算法。分治法是很多高效算法的基础,如快速排序,归并排序,傅立叶变换(快速傅立叶变换)等等。
例子
下面通过一个例子来看看快速排序是怎么工作的,例子中表格中红色的字体为需要填的坑,绿色的字体为已经移动过的数据。

1)刚开始,i 和 j 分别指向数组头和数组尾,即 i = 0,j = 9,基准数取第一个数,即 index = array[i] = array[0] = 23。
此时,array[0] 的值已经存在了index,因此 array[0] 的位置就好像被挖了个坑,可以填充一个数。
因此,我们从位置 j 开始向左寻找比 index 小的数,当 j = 8 时,符合条件,于是我们将 array[8] 的值填到 array[0] ,即将 9 填入 array[0],并将 i 向右移动一个位置,即 i++。
从位置 j 向左寻找比 index 小的数,并在寻找到后填入坑中,用代码表示如下。
while (i < j && array[j] >= index) { // 向左寻找第一个小于index的数
j--;
}
if (i < j) {
array[i++] = array[j]; // 将array[j]填入array[i],并将i向右移动
}
此时,array 数组如下图。

2)因为 array[0] 的坑被 array[8] 填了,于是 array[8] 的位置又成了一个新的坑。此时我们从位置 i 开始向右寻找比 index 大的数,当 i = 2 时符合条件,于是我们将 array[2] 的值填到 array[8] ,即将 37 填入 array[8],并将 j 向左移动一个位置,即 j--。
从位置 i 向右寻找比 index 大的数,并在寻找到后填入坑中,用代码表示如下(跟上面相似)。
while (i < j && array[i] < index) {// 向右寻找第一个大于index的数
i++;
}
if (i < j) {
array[j--] = array[i]; // 将array[i]填入array[j],并将j向左移动
}
此时,array 数组如下图。

以之后重复上述过程即可。
3)同样的,array[8] 的坑被 array[2] 填了,于是 array[2] 的位置又成了一个新的坑。此时我们从位置 j 开始向左寻找比 index 小的数,当 j = 5 时符合条件,于是我们将 array[5] 的值填到 array[2] ,即将 21 填入 array[2],并将 i 向右移动一个位置,即 i++,

此时 array 数组如下图。
4)同样的,array[2] 的坑被 array[5] 填了,于是 array[5] 的位置又成了一个新的坑。此时我们从位置 i 开始向右寻找比 index 大的数,当 i = 3 时符合条件,于是我们将 array[3] 的值填到 array[5] ,即将 89 填入 array[5],并将 j 向左移动一个位置,即 j--,

此时 array 数组如下图。
5)同样的,array[5] 的坑被 array[3] 填了,于是 array[3] 的位置又成了一个新的坑。此时我们从位置 j 开始向左寻找比 index 小的数,当 j = 4 时符合条件,于是我们将 array[4] 的值填到 array[3] ,即将 2 填入 array[3],并将 i 向右移动一个位置,即 i++,

此时 array 数组如下图。
6)此时,我们发现 i = j,结束遍历,并将index填入 array[4],即将 23 填入 array[4],此时 array 数组如下图。此时,array[4] 左边的数据全比 array[4] 小,而 array[4] 右边的数据全比 array[4] 大。

7)接下去,我们只需要对 array[4] 两边的数据分别在进行上面的操作即可(分治法),如下图。
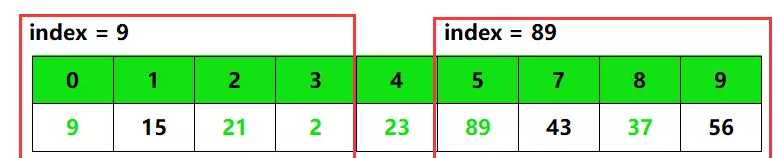
分治的代码可以写成如下:
quickSort(array, low, i - 1); // 递归调用,分治
quickSort(array, i + 1, high); // 递归调用,分治
整合
根据以上步骤,稍微整理一下,可以得出快速排序的代码如下:
public class QuickSort {
private static void quickSort(int[] array, int low, int high) {
if (low >= high) {
return;
}
int i = low, j = high, index = array[i]; // 取最左边的数作为基准数
while (i < j) {
while (i < j && array[j] >= index) { // 向左寻找第一个小于index的数
j--;
}
if (i < j) {
array[i++] = array[j]; // 将array[j]填入array[i],并将i向右移动
}
while (i < j && array[i] < index) {// 向右寻找第一个大于index的数
i++;
}
if (i < j) {
array[j--] = array[i]; // 将array[i]填入array[j],并将j向左移动
}
}
array[i] = index; // 将基准数填入最后的坑
quickSort(array, low, i - 1); // 递归调用,分治
quickSort(array, i + 1, high); // 递归调用,分治
}
public static void quickSort(int[] array) {
if (array == null || array.length == 0) {
return;
}
quickSort(array, 0, array.length - 1);
}
}
时间复杂度
最好情况的时间复杂度为O(nlogn),过程比较复杂,就不在此赘述。
最差情况下每一次取到的数(基准数)都是当前要比较的数中的最大/最小值,在这种情况下,每次都只能得到比上一次少1个数的子序列(即要么全比基准数大,要么全比基准小),此时相当于一个冒泡排序,比较的次数 = (n - 1) + (n - 2) + ... + 2 + 1 = (n - 1) * n / 2,此时的时间复杂度为:O(n^2)。最差情况一般出现在:待排序的数据本身已经是正序或反序排好了。
使用场景
基本上在任何需要排序的场景都可以使用快速排序。虽然快速排序的最坏情况时间复杂度为O(n^2),但是由于基本不会出现,因此可以放心的使用快速排序。在本人的电脑测试,100万的随机数字,快速排序大约耗时120毫秒。
最后
理解了快速排序的基本思想后,手写快速排序算法就变得没那么难了,只需要多练习几遍,相信在面试中手写快速排序算法便是小菜一碟。

 2021-03-26 06:29:41
2021-03-26 06:29:41












