2021-11-05 23:05:55
一、集合符号
1、集合与元素之间
符号“”表示“属于”；符号“”表示“不属于”，符号“P(x)”表示“元素x具有性质P”。
设a为集合，x为元素。例如：
X A:表示元素x属于A。
x:表示元素x不属于.
{x x a，p (x)}:集合a中所有属性为p的元素x。
2、集合之间
符号“”表示“包含”；Match "="表示"相等"；匹配“”表示“空集合”；
符号“”表示“联合”或“和”；符号“”表示“交叉”或“相乘”；
符合“-”表示“差”或“多”。
设 A 与 B 是两个集合 ，例如 ：
B:表示A中的任何元素X都是B的元素，或者A是B的子集，或者A被B包含。
A=B:表示A和B相等，即A和B都是B和A。
AB:表示a和b的并集或和集，即AB={x xA或xB}。
ab:表示a和b的交集或乘积集，即ab={ x xa和xB}。
ab:表示a和b的差集或余数集，即ab={ xxa和x B}。
二、数集符号
r:表示“实数集”；q:代表“有理数集”；z:代表“整数集”；n:表示“正整数集”。
.
1、区间 （a , b R , 且 a b）
有限区间
(a，b):表示“开放区间”，{x a x b}。
[a，b]:表示“封闭区间”，{x a x b}。
(a，b):表示“半开区间”，{ xa & lt；x b}。
[a，b]:表示“半开区间”，{ xax & lt；b}。
无限区间
(a，):表示“开放区间”，{x a x}。
[a，]:表示“封闭区间”，{x a x}。
(-，a):表示“开放区间”，{ xx & lt；a}。
[，a]:表示“封闭区间”，{x x a}。
三、逻辑符号
1、连词符号
连接符号图(1)
设a和b是两个陈述句，可以是条件，也可以是命题。例如：
连接符号图(2)
包含和不包含符号大全）" src="/uploads/allimg/211105/2305552950-4.png">
连词符号图（3）
2、量词符号
量词符号图（1）
应用上述的数理逻辑符号表述定义、定理比较简练明确。
例如：数集 A 有上界、有下界和有界的定义：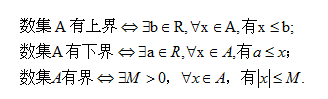
量词符号图（2）
四、其它符号
符号 “max” 表示 “最大” ；
符号 “min” 表示 “最小” 。
其它符号图（1）
符号 “n!” 表示 “ n 的阶乘 ”，即：n! = n · ( n – 1 ) ··· 3 · 2 · 1 ;
例如：5！ = 5 · 4 · 3 · 2 · 1 ，规定：0！= 1 。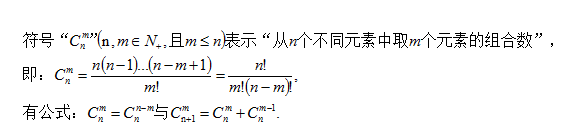
其它符号图（2）
下一篇：没有了
